HKUST COMP4901U Computer Language Processing and Compiler Design
introduction
-
a language can be natural language, computer language, language of mathematics
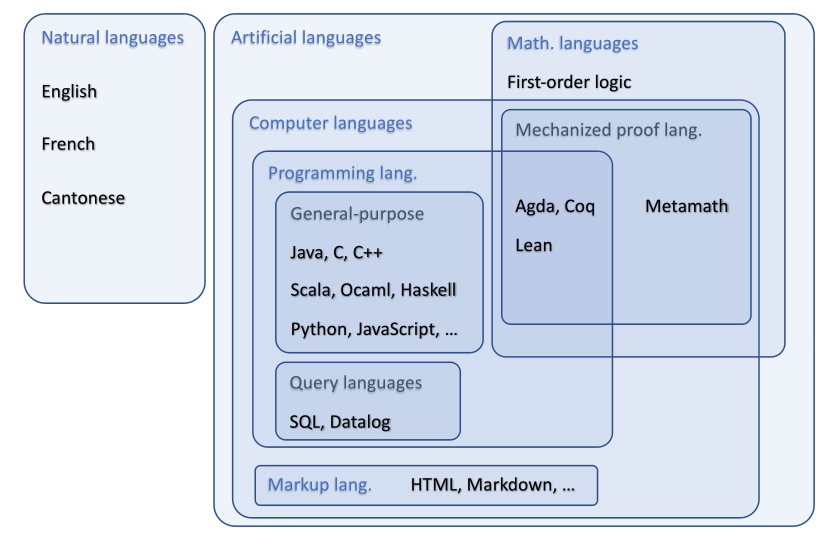
-
processing general-purpose programming languages:
- interpreter: execute instructions while traversing the program (Python)
- compiler: traverse program, generate executable code to run later (Rust, C)
-
general compiler organization
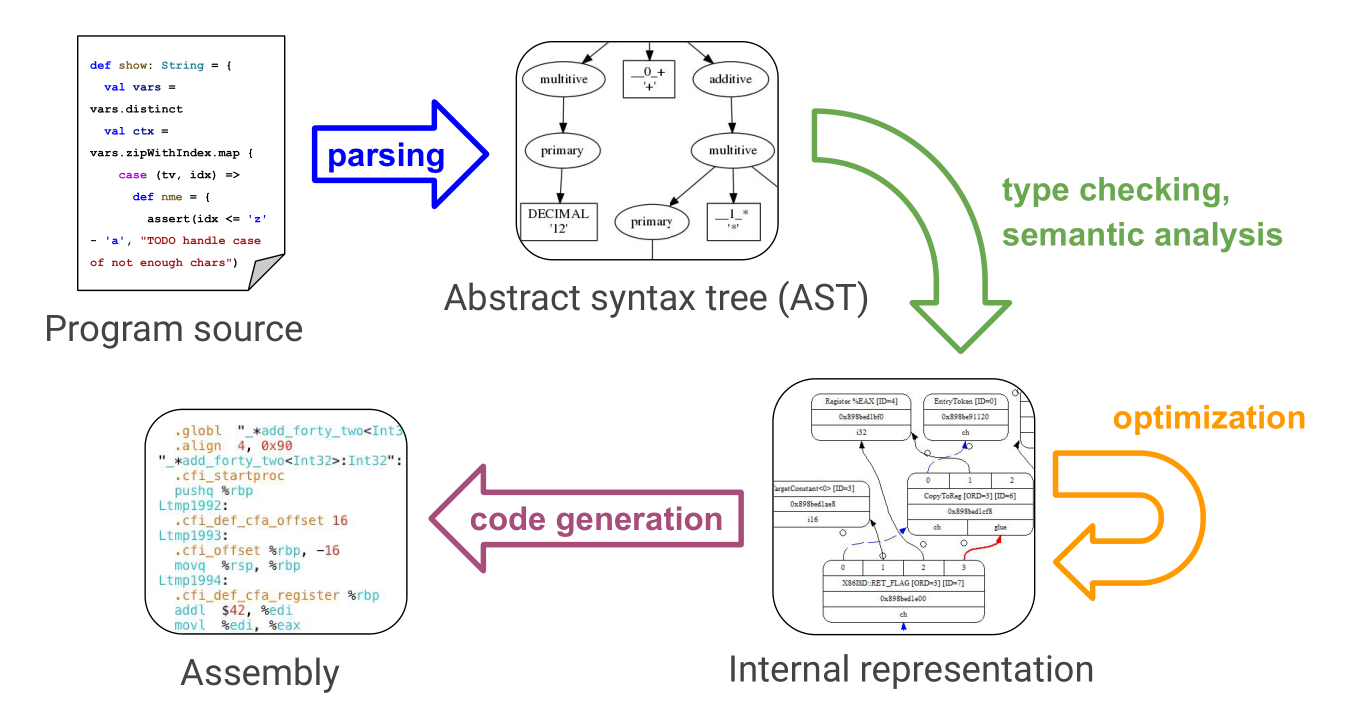
- source code: for programmers, higher level for abstraction and productiveness
- target code: efficiently run on hardware, low level
-
front end & back end in compiler
front-end —————————————————————————–> back-end
lexical analyzer -> parser -> name analyzer -> type checker -> intermediate code generator -> JIT compiler or platform-specific back end
-
program first to a tree structure, Abstract Syntax Tree (AST)
- node represents arithmetic operations, statements, blocks
- leaves represent constants, variables, methods
theory of formal languages
word
define of word
Let A be an alphabet {a, b, c, …}
define words of length n, as A^n^, as follow:
- A^0^ = ${\epsilon}$, only one word of length 0
-
For n > 0, $A^n = {aw w\in A^{n-1}}$
set of all words: $A^* = \cup_{n \ge 0}A^n$
equivalent word
Let $u,v \in A^*$, then u=v if and only if
- $u=\epsilon \text{ and } v = \epsilon$; or
- $u=au^\prime ~ and ~ v = av^\prime ~ where ~ u^\prime = v^\prime$
Theorem (Structural induction of words)
$P(\epsilon)$ , P(u) implies P(au), then for any word a, P(a) is correct
word concatenation
$ u \cdot v = \left{
\begin{array}{ c l }
v & \text{if } u=\epsilon
a(u^\prime \cdot v) & \text{if } u = au^\prime
\end{array}
\right. $
for easy notation, uv means word concatenation

free monoid of words
an algebraic structure, word monoid satisfies two additional properties:
- left cancellation law, if wu = wv, then u = v
- right cancellation law
reversal

prefix, suffix, and slice
easy as name extends
language
define of language
a language over alphabet A is a set $L \subseteq A^\prime$, for example A = {0, 1}
- a finite language like L={0, 1, 01, 010}, or the empty language $\empty$
- infinite but very difficult to describe
- infinite but having some nice structure, a pattern for description precisely
| for example, $L_2=\set{01, 0101, 010101, …} = \set{(01)^n | n\ge1}$ |
language is a set, we have union, intersection, and other set operations
language operations


monoid of language
two conditions for monoid
- a neutral element, $L\set{\epsilon}=L,\set{\epsilon}L=L, \text{ so } \set{\epsilon}$ is one
- associative law: we need $L_1 \cdot (L_2 \cdot L_3)=(L_1 \cdot L_2) \cdot L_3$

note: no cancellation law! $L_1\empty = \empty = L_2 \empty$ but not necessarily L1=L2
represent programming language
in general, some formal languages are not recursively enumerable sets
a language $L \subseteq A^$ is given by its characteristic function $f_L : A^\to \set{0,1}$, defined by f~L~(w) = 1 for w in L, and 0 for w not in L
| for example, for $L_2=\set{01, 0101, 010101, …} = \set{(01)^n | n\ge1}$ |
def f(w: List[Int]): Boolean = w match
case Cons(0, Cons(1, Nil())) => true
case Cons(0, Cons(1, wRest)) => f(wRest)
case _ => false
val L2 = Lang(f)
L2.contains(0::1::0::1::Nil()) // true
Kleene Star, repetition of a language

regular expression
one way to denote (often infinite) languages
definition
a regular expression e is built from:
- $\empty$, corresponds to the empty language
- $\epsilon$, corresponding to $\set{\epsilon}$
- a, b, etc. corresponding to $\set{a}, \set{b},…$
-
e1 e2 corresponding to $L_{e1} \cup L_{e2}$ - e1e2, corresponding to $L_{e1} \cdot L_{e2}$
- e* corresponding to $L_{e}^{*}$
regular expression operators
-
[a…z] = a b … z -
e^?^ = e $\epsilon$ - e^+^ = e e^*^
- e^k..^ = e^k^ e^^ and e^p..q^ = e^p^ (e^?^)^q-p^
- !e, complementary, no obvious translation from base oprators
-
e1 & e2 = ! (!e1 !e2), denoting $L_{e1} \cap L_{e2}$
properties of regular expression
emptiness, inclusion, disjointness
lexical Analysis
input: character streams. res = 14 + arg * 3
output: token streams. “res”, “=”, “14”, “+”, “arg”, “*”, “3”
key ideas:
- small memory usage
- not difficult to construct manually
- use longest match rule
lexer is implemented by:
- conversion to finite-state automata
- usage of regular expression derivation
example of a simple lexer:
num = 13;
while (num > 1) {
println("num = ", num);
if (num % 2 == 0) {
num = num / 2;
} else {
num = 3 * num + 1;
}
}
tokens:
Ident ::=
letter (letter | digit)*
integerConst ::=
digit digit*
keywords
if else while println
special symbols
( ) && < == + - * / % ! - { } ; ,
letter ::= a | b | c | … | z | A | B | C | … | Z
digit ::= 0 | 1 | … | 8 | 9
a small hand-written lexer:
enum Token:
case ID(content: String) // id3
case IntConst(value: Int) // 10
case object AssignEQ
case CompareEQ
case MUL // *
case PLUS // +
case LEQ // <=
case OPAREN
case CPAREN
case IF
case WHILE
case EOF // End Of File
class CharStream(fileName: String):
val file = new BufferedReader(
new FileReader(fileName))
var current: Char = '\0x0'
var eof: Boolean = false
def next =
if (eof)
throw EndOfInput("reading" + file)
val c = file.read()
eof = (c == -1)
current = c.toChar
next // initialize first char
class Lexer(ch: CharStream):
var current: Token
def next: Unit =
// lexer code goes here
if (isLetter) {
b = new StringBuffer
while (isLetter || isDigit) {
b.append(ch.current)
ch.next
}
keywords.lookup(b.toString) {
case None=> token=ID(b.toString)
case Some(kw) => token=kw
}
}
if (isDigit) {
k = 0
while (isDigit) {
k = 10*k + toDigit(ch.current)
ch.next
}
token = IntConst(k)
}
deciding which token is coming
problem: how do we know we are analyzing a string or integer sequence?
first
use first(e) - symbols with which e can start
$first(L) = \set{a \in A \mid \exist v \in A^*. ~ av\in L }$
example: L = {a, ab}, first(L) = {a}
first($\empty$) = $\empty$
first($\epsilon$) = $\empty$
first(a) = {a}
| first(e1 | e2) = first(e1) $\cup$ first(e2) |
first(e^*^) = first(e)
first(e1e2) = $\text{if }(nullable(e1))\text{ then }first(e1) \cup first(e2) \text{ else } first(e1)$
nullable
nullable($\empty$) = false
nullable($\epsilon$) = true
nullable(a) = false
| nullable(e1 | e2) = nullable(e1) $\or$ nullable(e2) |
nullable(e^*^) = true
nullable(e1e2) = nullable(e1) $\and$ nullable(e2)

ch.current match {
case '(' => {current = OPAREN; ch.next; return}
case ')' => {current = CPAREN; ch.next; return}
case '+' => {current = PLUS; ch.next; return}
case '/' => {current = DIV; ch.next; return}
case '*' => {current = MUL; ch.next; return}
case '=' => { // more tricky because there can be =, �==
ch.next
if (ch.current �== '=') {ch.next; current = CompareEQ; return}
else {current = AssignEQ; return}
}
case '<' => { // more tricky because there can be <, <=
ch.next
if (ch.current == '=') {ch.next; current = LEQ; return}
else {current = LESS; return}
}
}
longest match rule

token priority
for a word is both identifier and keyword, which should we assign? Set a priority so match the keyword first
general approach to automatic lexing
traditional approach
- convert to nondeterministic finite-state automaton
- perform determinization (can be expensive)
- run the resulting automaton on input (linear in the input size)
Brzozowskis derivatives
accepts: (e, w) -> {true, false} e: regular expression, w: input word
accepts(e, epsilon) = nullable(e)
accepts(e, cu) =
if e = null, false
if e = epsilon, false
if e = c, if(u = epsilon) true else false
if e = d, false
if e = e1 | e2, accepts(e1, w) || accepts(e2, w)
if e = e1e2, ??? // need to try all splits of w?
if e = e1*, ???
after consume a given letter, what is the rest of the regex?
definition:
The derivative of a regex e with respect to letter c, written as $\delta^c(e)$, is defined as:
$L(\delta^c(e)) = \set{w \mid cw \in L(e)}$
the derivative of a regex is still a regex
some examples:
| $\delta^a(ab | ac | da)=b | c$ |
$\delta^a((ab)^)=b(ab)^$
| $\delta^a((ab | c)^*ad)=b(ab | c)^*ad \mid d$ |
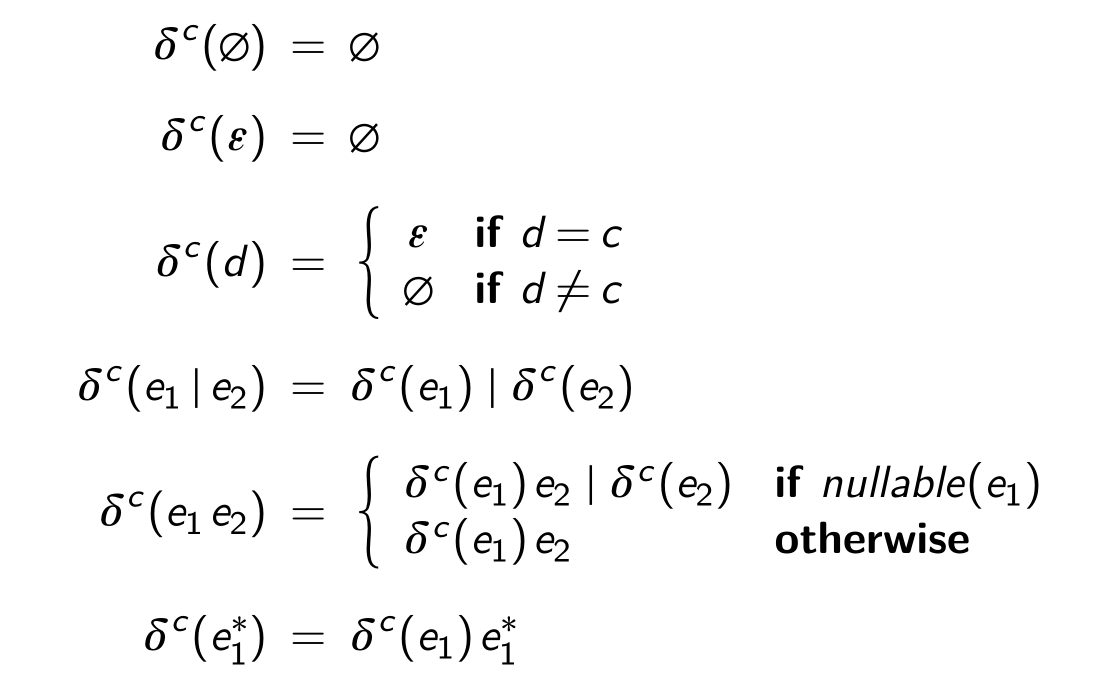
matching regex by derivation
accepts: (e, w) -> {true, false} e: regular expression, w: input word
accepts(e, epsilon) = nullable(e)
accepts(e, cw) = accepts($\delta^c(e)$, w)
Important: need to cache each intermediate result to avoid duplicate calculation
regular expression in Scala
enum RegExp:
// empty language∅
case Failure
// empty wordϵ
case EmptyStr
// character a such that predicate(a)
case CharWhere(predicate: Character => Boolean)
// union left|right
case Union(left: RegExp, right: RegExp)
// concatenation first|second
case Concat(first: RegExp, second: RegExp)
// Kleene star underlying∗
case Star(underlying: RegExp)
// is this regexp nullable?
def acceptsEmpty: Boolean = ...
// can this regexp possibly accept some words?
def isProductive: Boolean = this match
case Failure => false
case EmptyStr | CharWhere(_) | Star(_) => true // approx.
case Union(l, r) => l.isProductive || r.isProductive
case Concat(l, r) => l.isProductive && r.isProductive
extension (expr: RegExpr):
def ~ (that: RegExpr): RegExpr = Concat(expr, that)
def | (that: RegExpr): RegExpr = Union(expr, that)
def * : RegExpr = Star(expr)
def ? : RegExpr = expr | EmptyStr
def + : RegExpr = expr ~ expr.*
def times(n: Int): RegExpr =
if (n <= 0) EmptyStr else expr ~ expr.times(n - 1) }
// example
// e1 ~ e2 ~ e3 | e4
// e1.* | e2.+
def elem(pred: Char => Boolean): RegExpr = CharWhere(pred)
def elem(char: Char): RegExpr = CharWhere(_ == char)
def elem(chars: Iterable[Char]): RegExpr =
chars.map(elem).foldLeft[RegExpr](Failure)(_ | _)
def word(chars: Iterable[Char]): RegExpr =
chars.map(elem).foldLeft[RegExpr](EmptyStr)(_ ~ _)
def inRange(low: Char, high: Char): RegExpr =
elem(c => c >= low && c <= high)
// Example:
elem(_.isLetter) ~ (elem(_.isLetter) | elem(_.isDigit)).*
def derive(char: Character): RegExp =
def work(expr: RegExp): RegExp = expr match
case Failure | EmptyStr => Failure
case CharWhere(pred) =>
if(pred(char)) EmptyStr else Failure
case Union(left, right) => work(left) | work(right)
case Concat(left, right) =>
val w = work(left) ~ right
if(left.acceptsEmpty) w | work(right) else w
case Star(inner) => work(inner) ~ expr
work(this)
naïve derivation is inefficient

solution: on-the-fly normalization
- associate all concatenation to the right: (e1e2)e3 => e1(e2e3)
-
avoid repetitions in unions: (e1 e2) (e2 e3) => e1 e2 e3
after removal,
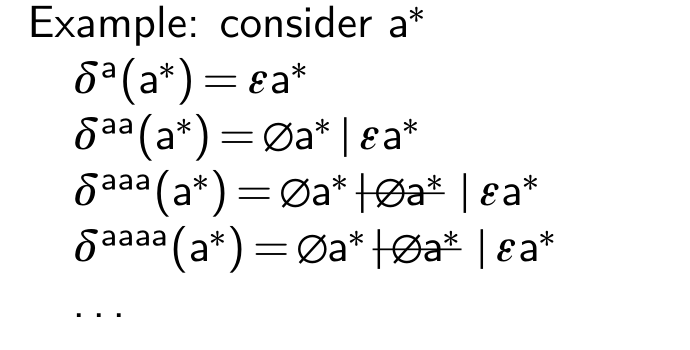
code:
def deriveNorm(char: Character): RegExp =
val disjuncted = collection.mutable.SortedSet[RegExp]()
def work(expr: RegExp, rest: RegExp): Unit = expr match
case CharWhere(pred) => if(pred(char)) disjuncted += rest
case Union(left, right) => work(left, rest); work(right, rest)
case Concat(left, right) =>
work(left, right ~ rest)
if(left.acceptsEmpty) work(right, rest)
case Star(inner) => work(inner, expr ~ rest)
case Failure | EmptyStr => ()
work(this, EmptyStr) // register unions into `disjuncted`
disjuncted.foldLeft[RegExp](Failure)(_ | _) // rebuild regexp
the pumping lemma
regular expression: though infinite, they contain a simple repeating pattern
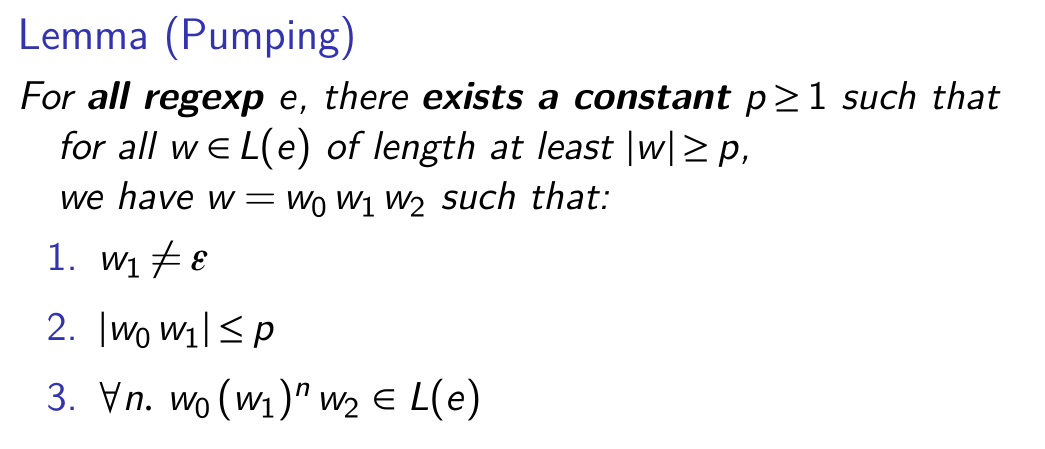
theory of normalizing derivation
this part is where I cannot understand.




Thus, number of distinct regexs generated by normalizing derivation of any w is bounded!
more specifically, for any e, we have:
| $ | \set{\underline\delta^w(e) \mid w \in A^*} | \le 1+2^{ | max(e, \epsilon) | }$ |
this allows regex matching in constant space and linear time w.r.t. size of words
algorithm for regex matching
- start with empty mapping M := $\empty$ and with regex e
- For each i^th^ character in c~i~ in w
- if (e, c~i~) not in domain(M), set M(e, c~i~) := $\underline\delta^{c_i}(e)$
- set e := M(e, c~i~)
- Test whether nullable(e)
expressiveness limitation of regex

grammars
regular grammar
an equivalent way of defining regular languages
| start -> letter(letter | digit)* |
letter -> [a..z]
| digit -> 0 | 1 | … | 9 |
regularity requirement: no recursion!
definitions form a directed acyclic graph (DAG)
context free grammar
$S \rightarrow \epsilon \mid a~S~b$
semantics given by rewriting derivations
S -> aSb -> aaSbb -> aaaSbbb -> aaa(epsilon)bbb = aaabbb
definition of a Context-Free Grammars (CFG)
a tuple G = (A, N, S, R)
- A - terminals (usually tokens, endpoint)
- N - non-terminals (symbols with recursive definitions)
- R - grammar rules as pair n -> v, where n is a non-terminal, $v \in (A \cup N)^*$
- S - starting symbol S
- G - the derivation starts from S
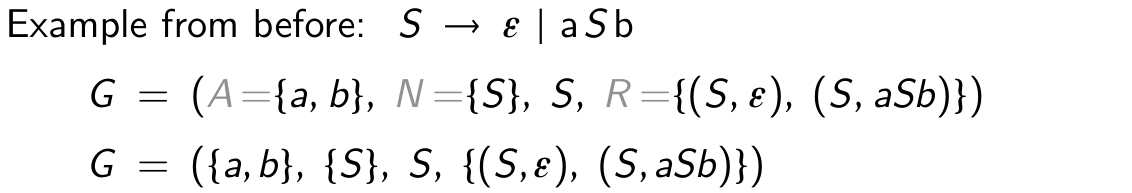
parse trees
definition
a tree t is a parse tree of G = (A, N, S, R) iff t is a node-labelled tree with ordered children that satisfies:
-
root is labeled by S
-
leaves are labelled by elements of A
-
each non-leaf node is labelled by an element of N
-
for each non-leaf node labelled by n,
whose children left to right are p~1~, … p~k~
there is a rule (n -> p~1~ … p~k~) belongs to R
-
the yield of parse tree t: a word obtained by the leaves of t
-
the language of grammar G: defined as L(G) = {yield(t) t is a parse tree of G}
example
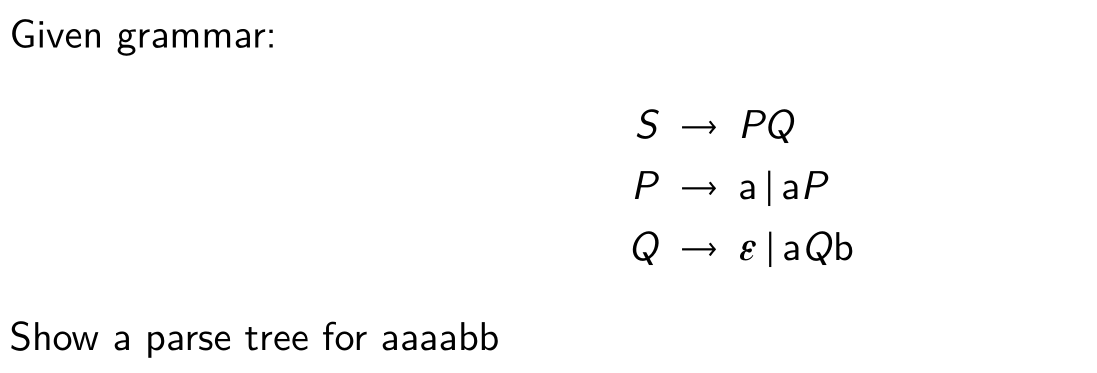

syntax tree
Difference between parse trees and abstract syntax trees
Node children in parse trees correspond precisely to RHS of grammar rules
- Definition of parse trees is fixed given the grammar. Often, compilers never actually build parse trees in memory
- uniquely specify how an input was recognized by the grammar
- contains all information needed to reconstruct the input
Nodes in abstract syntax tree (AST) contain only useful information
- We can choose our own syntax trees, to facilitate both construction and processing in later stages of compiler
Compilers often directly builds ASTs
ambiguous grammar
how to parse “x * 42 + y” ?
some token sequences have multiple parse trees => ambiguous

solution: change the grammar to layered form
| expr -> expr + expr | multi |
| multi -> intLiteral | ident | multi * multi | ’(‘ expr ‘)’ |
but how to parse “x + 42 + y” ?
we need to define the associative rule. For ‘+’, we want it to be left-associative, x+42+y = (x+42)+y
solution:
| expr -> expr + multi | multi |
| multi -> multi * factor | factor |
| factor -> intLiteral | indent | ’(‘ expr ‘)’ |
such a grammar is left recursive, since expr -> expr + …
generalities on grammar
Chomskys Classification of Grammars
- type 0, unrestricted: arbitrary string rewrite rules
- equivalent to Turing machines!
- eXb -> eXeX -> Y
- type 1, context sensitive: RHS always larger
- O(n)-space Turing machines
- aXb -> acXb
- type 2, context free: one LHS nonterminal
- X -> acXb
- type 3, regular: no recursion, just Kleene star
- X -> acY*b

parsing

recursive descent LL(1) parsing
- Can be easily implemented manually based on the grammar
- Efficient – linear in the size of the token sequence
- Direct correspondence between grammar and code
a simple example:
statmt ::=
println ( stringConst , ident )
| ident = expr
| if ( expr ) statmt (else statmt)?
| while ( expr ) statmt
| { statmt* }
a simple parser could be:
def skip(t : Token) = if (lexer.token == t) lexer.next
else error(“Expected”+ t)
def statmt = {
if (lexer.token == Println) { lexer.next;
skip(openParen); skip(stringConst); skip(comma);
skip(identifier); skip(closedParen)
} else if (lexer.token == Ident) { lexer.next;
skip(equality); expr
} else if (lexer.token == ifKeyword) { lexer.next;
skip(openParen); expr; skip(closedParen); statmt;
if (lexer.token == elseKeyword) { lexer.next; statmt }
} else if (lexer.token == whileKeyword) { lexer.next;
skip(openParen); expr; skip(closedParen); statmt
} else if (lexer.token == openBrace) { lexer.next;
while (isFirstOfStatmt) { statmt }
skip(closedBrace)
} else { error(“Unknown statement, found token ” + lexer.token) }
because we have terminals at the beginning of each alternative, which rule to parse is quite easy to get.
now look at another example:
%% the priority is similar to java
expr ::= expr ( +|-|*|/ ) expr
| name
| '(' expr ')'
name ::= ident
we can transform it to the abstract syntax tree:
expr ::= term termList
termList ::= + term termList
| - term termList
| epsilon
term ::= factor factorList
factorList ::= * factor factorList
| / factor factorList
| epsilon
factor ::= name | ( expr )
name ::= ident
corresponding code:
def expr = { term; termList }
def termList =
if (token==PLUS) {
skip(PLUS); term; termList
} else if (token==MINUS)
skip(MINUS); term; termList
}
def term = { factor; factorList }
...
def factor =
if (token==IDENT) name
else if (token==OPAR) {
skip(OPAR); expr; skip(CPAR)
} else error("expected ident or )")
we need to rewrite the AST so that:
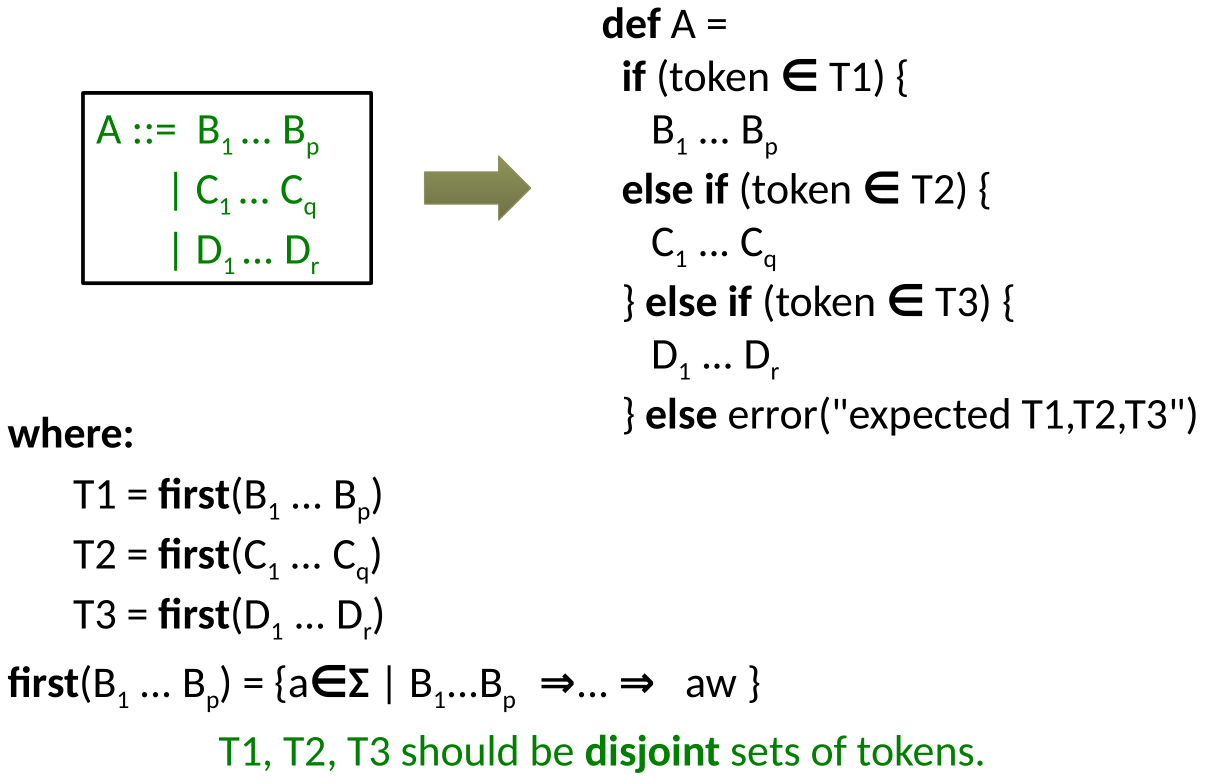
algorithm for first and null
$first(A) = first(B_1…B_p) \cup first(C_1…C_p) \cup first(D_1…D_p)$
$first(B_1…B_p) = \left{
\begin{array}{ c l }
first(B_1) & \text{if not } nullable(B_1)
first(B_1) \cup …\cup first(B_k) & \text{if } nullable(B_1),…, nullable(B_{k-1}) \text{ and not } nullable(B_k)
\end{array}
\right.$
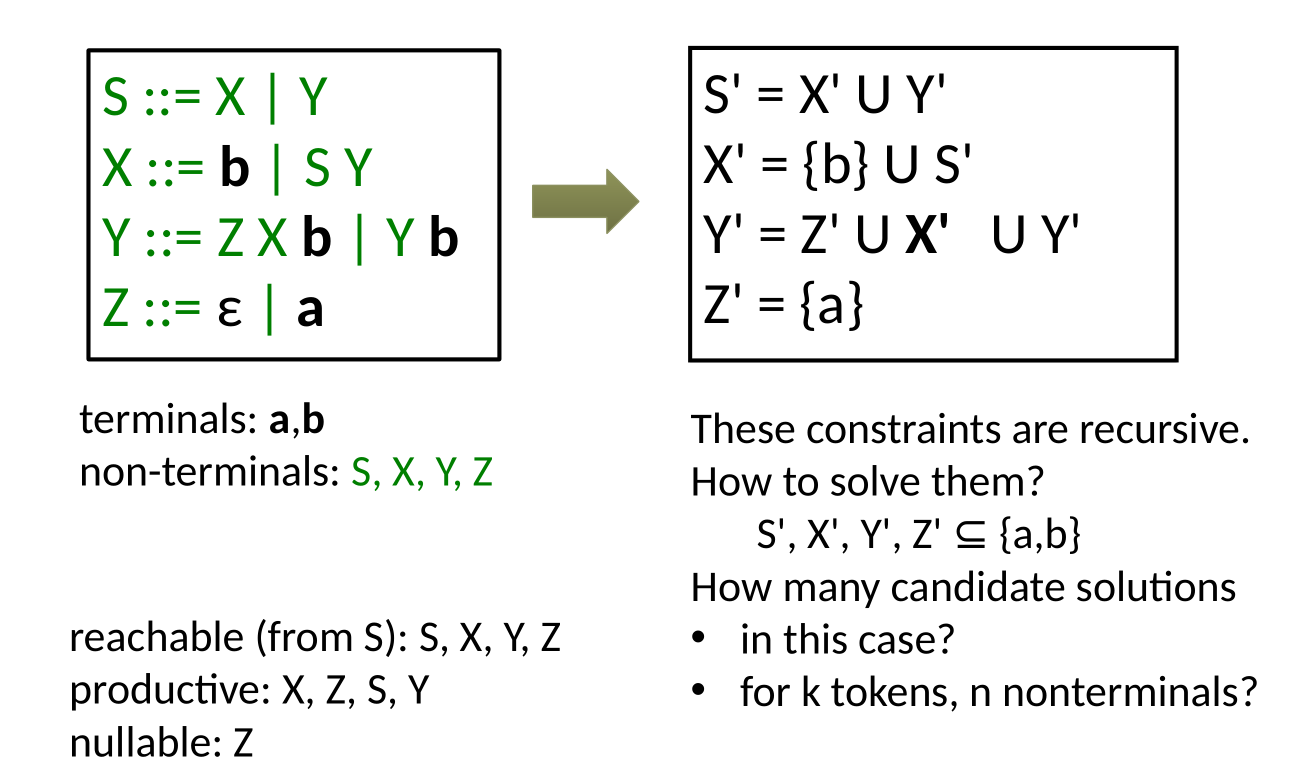

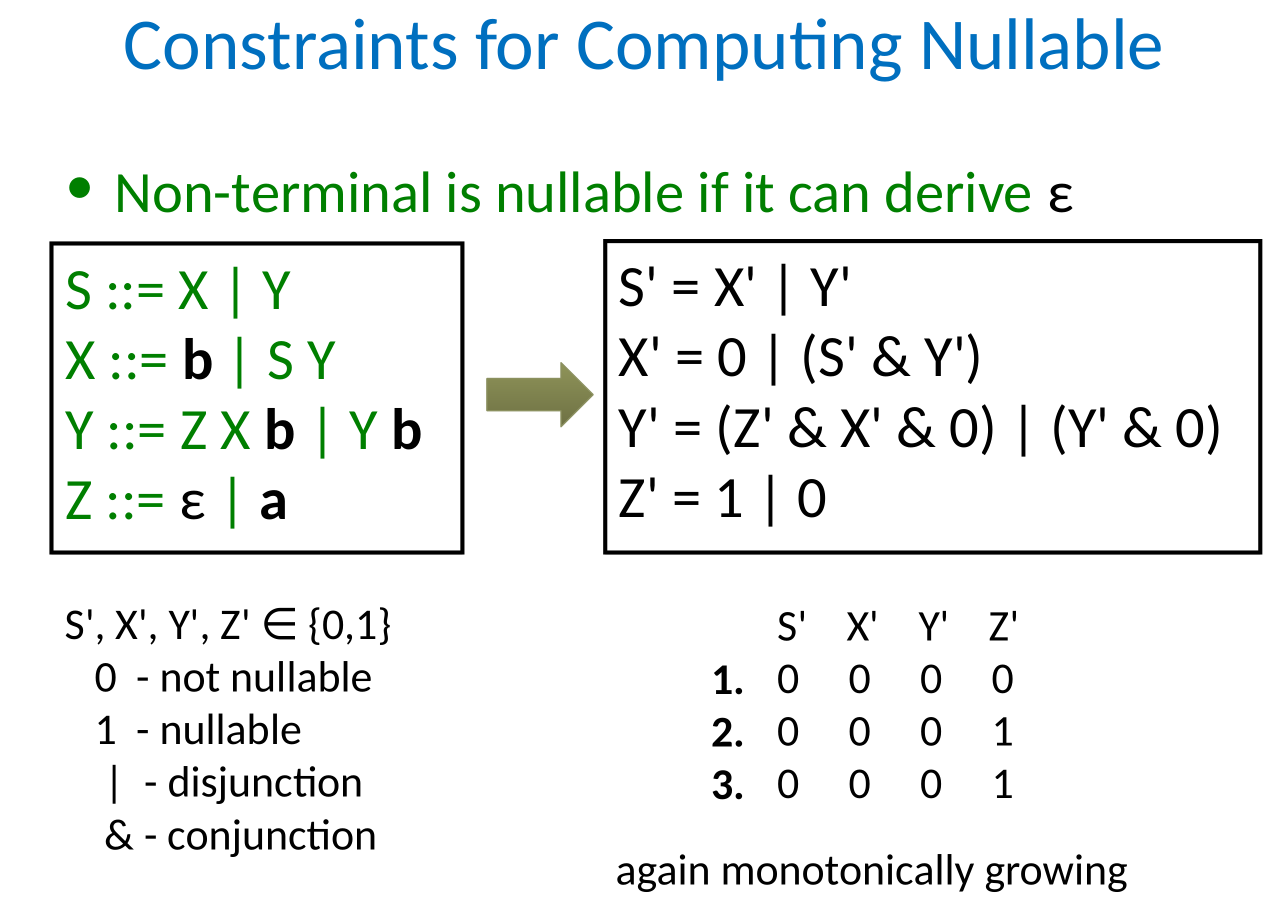
thus, given any grammar, we can:
- for each non-terminal X, whether nullable(X)
- using this, get the set of first(X) for each non-terminal
pseudo code for getting the constraints:
nullable = {}
changed = true
while (changed) {
changed = false
for each non-terminal X
if (X is not nullable) and (grammar contains rule X ::= ε | ... )
or (grammar contains rule X ::= Y1 ... Yn | ... where {Y1,...,Yn} in nullable)
then {
nullable = nullable U {X}
changed = true
}
}
for each nonterminal X: first(X) = {}
for each terminal t: first(t) = {t}
loop
for each grammar rule X ::= Y(1) ... Y(k)
for i = 1 to k
if i=1 or {Y(1),...,Y(i-1)} in nullable
then
first(X) = first(X) U first(Y(i))
until none of first(…) changed in last itera#on
problem with nullable non-terminal
there are still some cases cannot be determined only using first set:
stmtList ::= ε | stmt stmtList
stmt ::= assign | block
assign ::= ID = ID
block ::= beginof ID stmtList ID ends
def stmtList =
if (???) // what should the condition be?
else { stmt; stmtList }
def stmt =
if (lex.token == ID) assign
else if (lex.token == beginof) block
else error(“Syntax error: expected ID or beginonf”)
…
def block =
{ skip(beginof); skip(ID); stmtList; skip(ID); skip(ends) }
we cannot determine if stmtList is null or continue parsing:
For nullable non-terminals, we must also compute what follows them
parsing the block, beginof ID stmtList ID ends, after we consume beginof, ID, next we see is also an ID, what is this ID for? a new assignment? or the ID end? In LL(1) grammar, by just looking at next token, this is not determined!
LL(1) grammar
- Grammar is LL(1) if for each nonterminal X
- first sets of different alternatives of X are dijoint
- if nullable(X), first(X) must be disjoint from follow(X) and only one alternative of X maybe nullable
- For each LL(1) grammar we can build recursive-descent parser
- Each LL(1) grammar is unambiguous
- If a grammar is not LL(1), we can sometimes transform it into equivalent LL(1) grammar
So for the above stmtList example, it is not LL(1) because:
- nullable(stmtList)
- first(stmtList) = {ID, beginof}
- follow(stmtList) = {ID}
- $first(stmt) \cap follow(stmtList) = {ID}$
algorithm for follow

LL(1) parse table
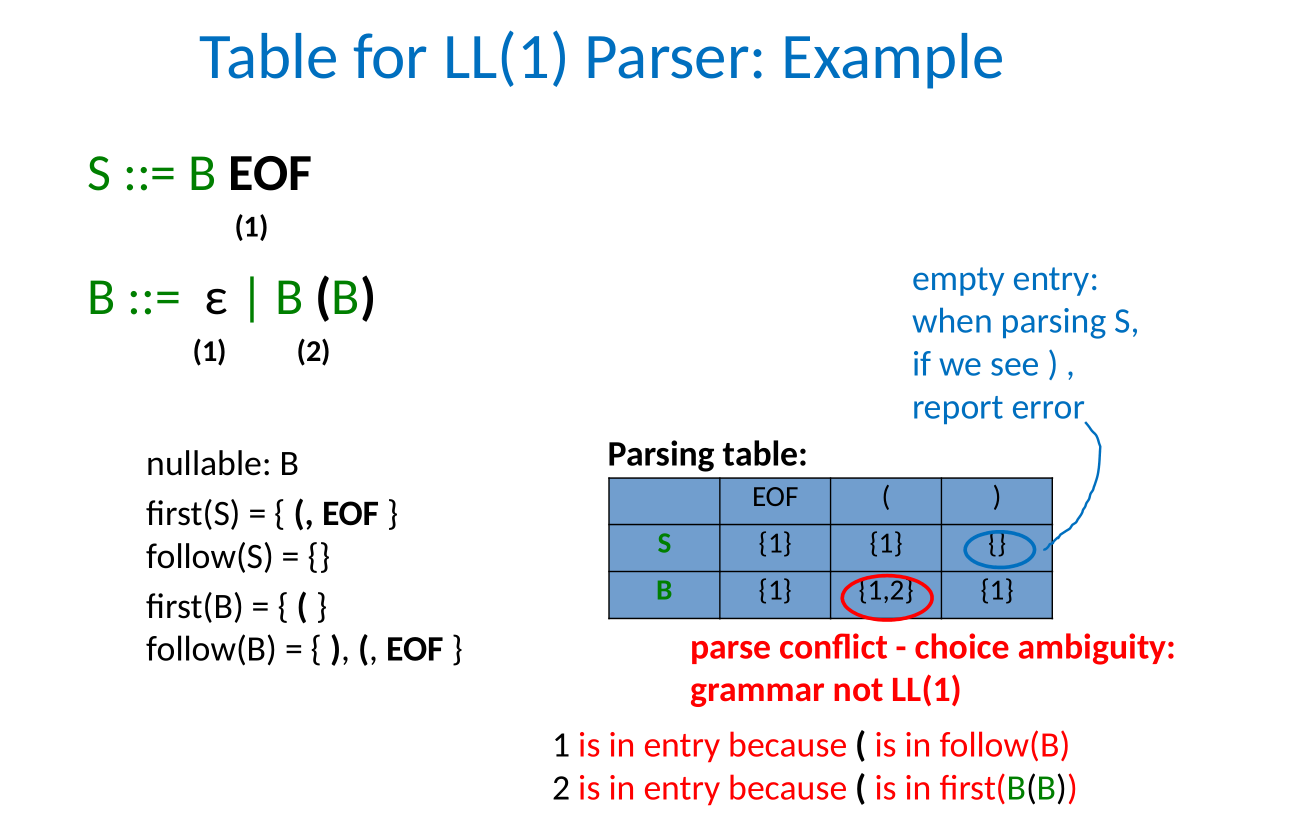
concrete parser implementation
enum Token:
case Ident(name: String)
case OpenParen
case CloseParen
case Plus
case Times
// "A + B * C" => Ident("A"),Plus,Ident("B"),Times,Ident("C")
enum Expr:
case Var(name: String)
case Add(lhs: Expr, rhs: Expr)
case Mult(lhs: Expr, rhs: Expr)
// "A + B * C" => Add( Var("A") , Mult(Var("B"), Var("C")) )
class Parser(ite: Iterator[Token]):
// Parser state manipulation:
var cur: Option[Token] = ite.nextOption
def consume: Unit =
cur = ite.nextOption
// define parser here:
def expr = ...
object Parser:
def parse(ts: Iterable[Token]): Expr =
val p = Parser(ts.iterator)
val res = p.expr // entry point
if (p.cur.nonEmpty)
fail("input not fully consumed")
res
// Helper method:
def skip(tk: Token): Unit =
if (cur != Some(tk))
fail("expected " + tk + ", found " + cur)
consume
// Unambiguous "atomic" expressions:
def atom: Expr =
cur match
case Some(Ident(nme)) =>
consume
Var(nme)
case OpenParen =>
consume
val e = expr
skip(CloseParen)
e
case _ => fail("expected atomic expression, found " + cur)
def expr: Expr =
val p = product
val ps = addedProducts
ps.foldLeft(p)((l, r) => Add(l, r))
def addedProducts: List[Expr] = \
cur match
case Some(Plus) =>
consume
product :: addedProducts
case _ => Nil
def product: Expr =
val a = atom
val as = multipliedAtoms
as.foldLeft(a)((l, r) => Mult(l, r))
def multipliedAtoms: List[Expr] = cur match
case Some(Times) =>
consume
product :: addedProducts
case _ => Nil
Pratt Parsing
how to avoid manually transforming grammars?
how to support user-defined operators and parse them correctly?
===> We need separately specify operator precedence / associativity
idea
Simplest way of describing precedence and associativity:
operators have distinct left and right precedences
‘+’ has (3,4) and ‘*’ has (5,6)
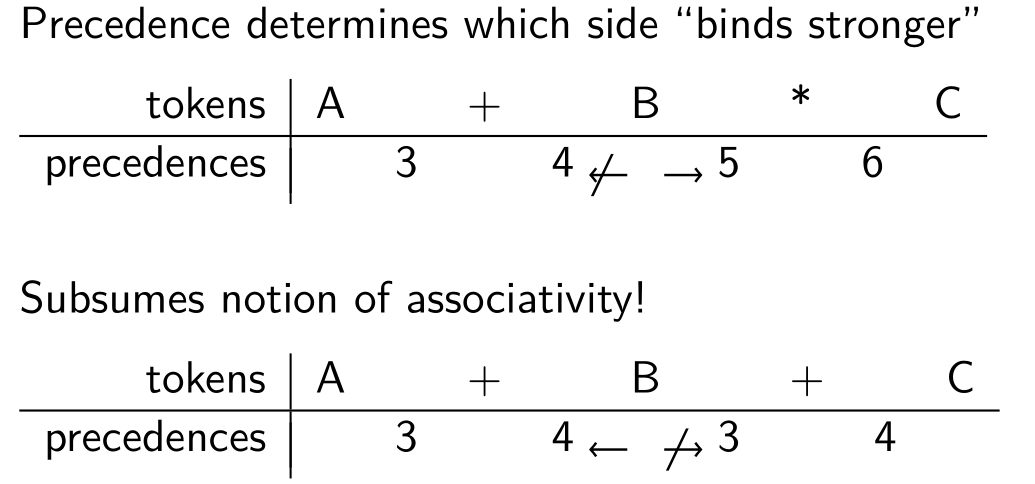
implementation
def opPrec(opStr: String): (Int, Int) = opStr match
case "*" => (50, 51)
case "+" => (30, 31)
case "=>" => (21, 20)
case ...
enum Token:
case OpenParen
case CloseParen
case Ident(name: String)
case Oper(name: String)
enum Expr:
case Var(name: String)
case Infix(lhs: Expr, op: String, rhs: Expr)
def expr(prec: Int): Expr =
cur match
case Some(Ident(nme)) =>
consume; exprCont(Var(nme), prec)
case Some(OpenParen) =>
consume; val res = expr(0); skip(CloseParen)
exprCont(res, prec)
case _ => fail(rest)
// Having parsed acc, what to do next at this precedence?
def exprCont(acc: Expr, prec: Int): Expr = cur match
case Some(Oper(opStr)) if opPrec(opStr)._1 > prec =>
consume
val rhs = expr(opPrec(opStr)._2)
exprCont(Infix(acc, opStr, rhs), prec)
case _ => acc
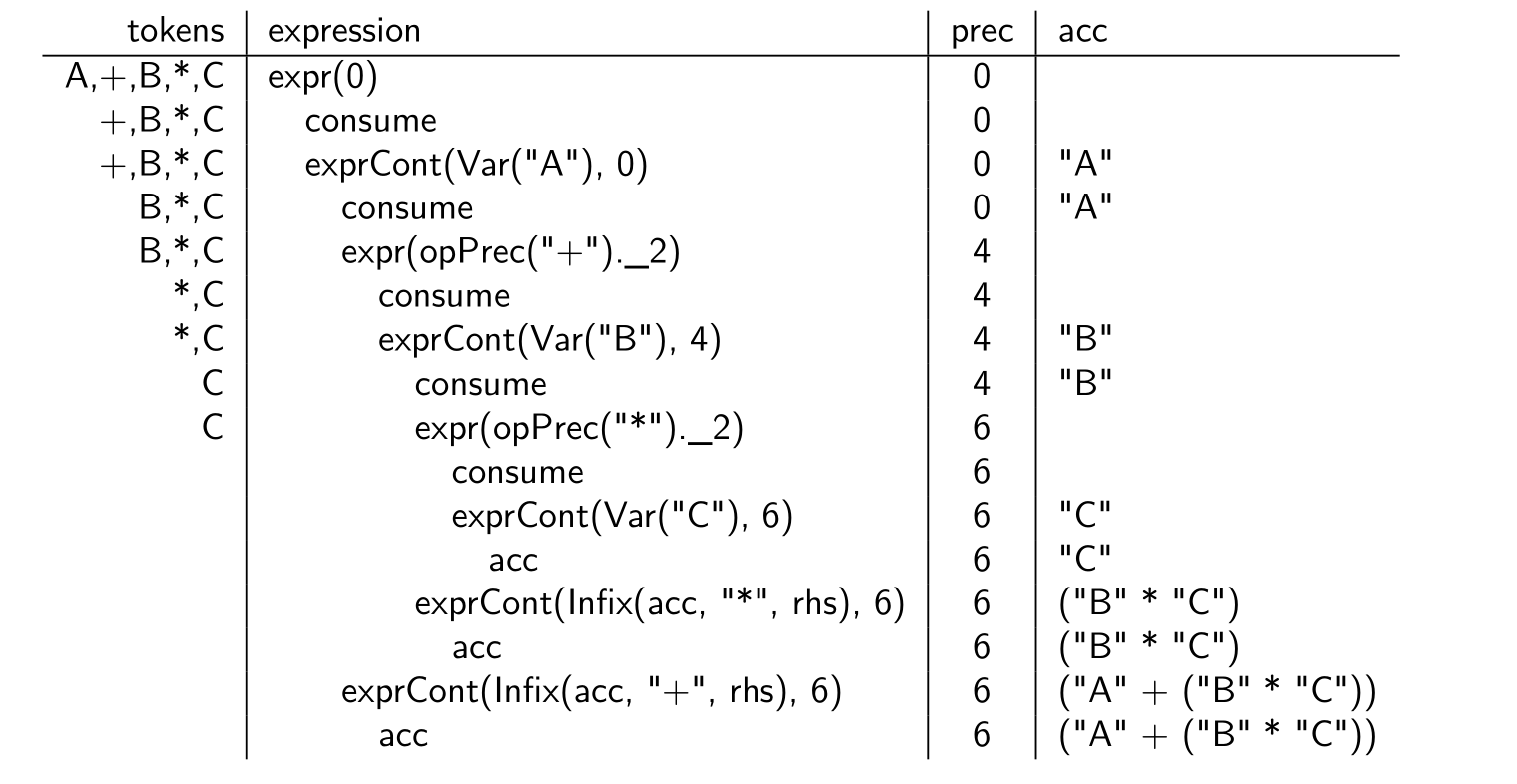
user defined operators
character precedence tables
parsing-expression grammars (PEG)
more recent alternative to context-free grammars (CFG) Parsing-Expression Grammars remove ambiguities through biased choice: Instead of X|Y, use X/Y which tries to parse Y only if parsing X fails!
name analysis

- An identifier is used but not declared: def p(amount: Int) { total = total + ammount }
- Multiple method arguments have the same name def p(x:Int, y:Int, x:Int) { FF. }
- Multiple functions with the same name object Program { def m(x: Int) = { x + 1 } def m(x: Int) = { x + 3 } }
- ill-formed type definition (e.g. circular) class List extends Expr class Cons extends List class Expr extends Cons
symbol table
maintain a map from identifiers to declaration information (symbol) at each point in the tree: symbol table
symbol tables can be computed every time, cached, or integrated partly or fully into trees as symbol reference
it provides efficient access to information of identifiers
- declaration of a value or variable, its type and initial value
- variable inside a pattern matching
- a function and its signatures and its body
- an algebraic data type (case class) its alternatives and fields
it is a map data structure
scope and scoping rules
static (lexical) scoping
local variables are only visible inside the function or block where they are introduced

type system
why type? prevent errors, ensure memory safety, document the program, refactor, compilation optimization
An unsound (broken) type system
background: inductively defined relations and sets

| proof that r = {(x, y) | x <= y}: |
-
if there is a derivation, then x<=y
- induction on derivation, go through each rule
-
if x<=y, there exists a derivation
-
given x, y find derivation tree
start from (0, 0) then derive (0, y-x) in y-x steps of increase right
if x > 0, increase both, x < 0, decrease both x times
-

context-free grammar as inductively defined relations

We define a rule as r of the form \(\frac{t_1(\bar x) \in r, ... , t_n(\bar x) \in r}{t(\bar x) \in r}\) where t~i~(x) in r is the assumptions, and t(x) in r is the conclusion
when n=0 (no assumptions), the rule is called an axiom
example: Amyli language
Amyli is a tiny language only works on integers and booleans
(initial) program is a pair (e~top~, t~top~) where
- e~top~ is the top-level environment, function names -> function definition
- t~top~ is the top-level term (expression) that starts execution
Function definition for a given function name is a tuple of:
- parameter list $\bar x$
- parameter type $\bar \tau$
- expression representing function body t
- result type $\tau_0$
expressions are formed by primitive functions (+, -, *, /), defined function calls or if expression
no local val definition nor match, e will remain fixed
thus, we can write t as: \(t := true \mid false \mid c \mid f(t_1, t_2, ..., t_n) \mid if (t) ~t_1 ~else ~t_2 \\ \text{c is an interger, f denotes user-defined function or primitive operators}\) so we can write a simple factor function program as:

operational semantics
so how can we process a program to infer its type? We need to define a set of rules so that we can define the relations inductively:




having these rules, we can do the induction:

now consider another example, when we encounter a expression: if (5) 3 else 7
5 cannot further evaluate and it is a integer constant, but if statement only accepts true, false, thus it get stuck
stuck terms indicate errors
Type checking is a way to prevent stuck terms statically, without trying to evaluate the program to see if it gets stuck
typing rules
typing context: given inital program (e, t) defined
\(\Gamma_0 = \set{(f, \tau_1 \times...\times\tau_n\to \tau_0)\mid (f, xs, (\tau_1,...,\tau_n), t_f, \tau_0)\in e}\)

now we can set the type rules for the Amyli language:

soundness theorem
if program type checks, its evaluation does not get stuck
proof using two lemmas (common approach):
-
progress
if a program type checks, it is not stuck.
if $\Gamma \vdash t:\tau$, then either t is a constant or there exists a t’ that $t \rightsquigarrow t’$
-
preservation
if a program type checks and makes one “$ \rightsquigarrow$” step, then the result again type checks.
e.g. if $\Gamma \vdash t:\tau$ and $t\rightsquigarrow t’$ then $\Gamma \vdash t’:\tau$
example: how to show that if is progress and preservation

don’t ask me why, I cannot understand this fucking tedious proof
an example of derivation tree:

type inference
motivation:
writing type annotations is boring, need a way to get the type automatically

then how to do a type inference? think about one small example:

strategy for type inference
- use type variable (e.g. $\alpha_{verbose}, \alpha_{s}$) to denote unknown types
- use type checking rules to derive constraints among type variables (e.g., arguments have expected types)
- use a unification algorithm to solve the constraints
demo using a simple language
types
- primitive types: Int, Bool, String, Unit
- type constructors: Pair[A, B] or (A, B), Function[A,B] or A=>B
Abstract syntax of types: \(T ::= Int \mid Bool \mid String \mid Unit \mid (T_1, T_2) \mid (T_1, \Rightarrow T_2)\) Terms include pairs and anonymous functions: (x denotes variables, c literals) \(t ::= x \mid c \mid f(t_1,...,t_n) \mid if (t) ~ t_1 ~ else ~ t_2 \mid (t1,t2) \mid (x \Rightarrow t)\) if t= (x,y) then t._1=x and t._2=y
type rules




now let’s see an example:
def translatorFactory(dx, dy) = {
p⇒(p._1 + dx, p._2 + dy)// returns anonymous function
}
def upTranslator = translatorFactory(0, 100)
def test = upTranslator((3, 5)) // computes (3, 105)
// the actual type should be:
def translatorFactory(dx: Int, dy: Int): (Int,Int) -> (Int,Int) = {
p⇒(p._1 + dx, p._2 + dy)
}
def upTranslator : (Int,Int) -> (Int,Int) = translatorFactory(0, 100)
def test: (Int,Int) = upTranslator((3, 5))
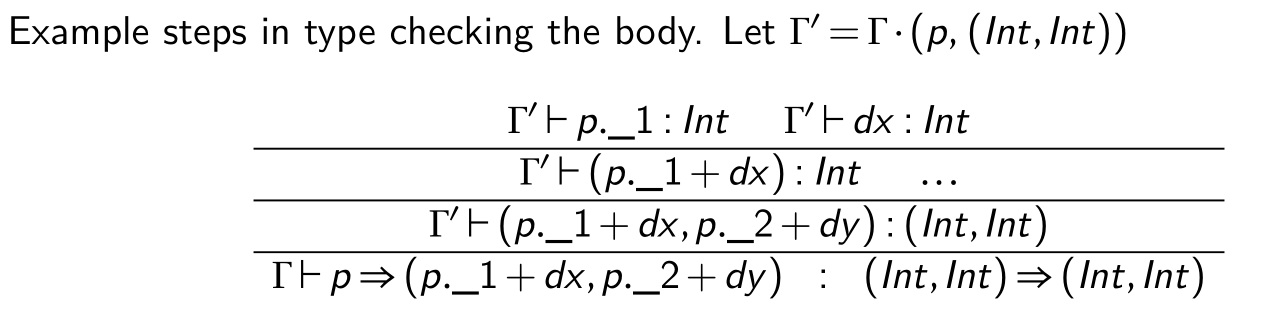
So, when we don’t have the type, how can we inference the type, say dx?
def translatorFactory(dx, dy) = { p⇒(p._1 + dx, p._2 + dy) }

so, we can generate constraints from the expressions given:

then, we need a unification algorithm to solve the constraints:
-
Apply following rules as long as current set of equations changes:
-
Orient: Replace T=αwithα=T when T not a type variable
-
Delete useless: Remove T=T (both sides syntactically equal)
-
Eliminate: Givenα=T whereαdoes not occur in T,
-
replaceαwith T in all remaining equations
-
Occurs check: Givenα=T whereαoccurs in T, report error (no solutions)
-
Decompose pairs: Replace(T1,T2) = (T′1,T′2)with T1=T′1and T2=T′2
-
Decompose functions: Replace(T1⇒T2) = (T′1⇒T′2)with T1=T′1and T2=T′2.
-
Decomposition clash (remaining cases): Given T1=T2 where T1and T2have different constructors, report clash (no solution)
Examples:(T1,T2) = (T′1⇒T′2); Int= (T1,T2); Int=Bool;(T1⇒T2) =String
-
-
property of unification algorithm
- always terminated
- If error reported, equations have no solution
- otherwise, it has one or more solutions
code generation

the specification for Web Assembly is at this link here
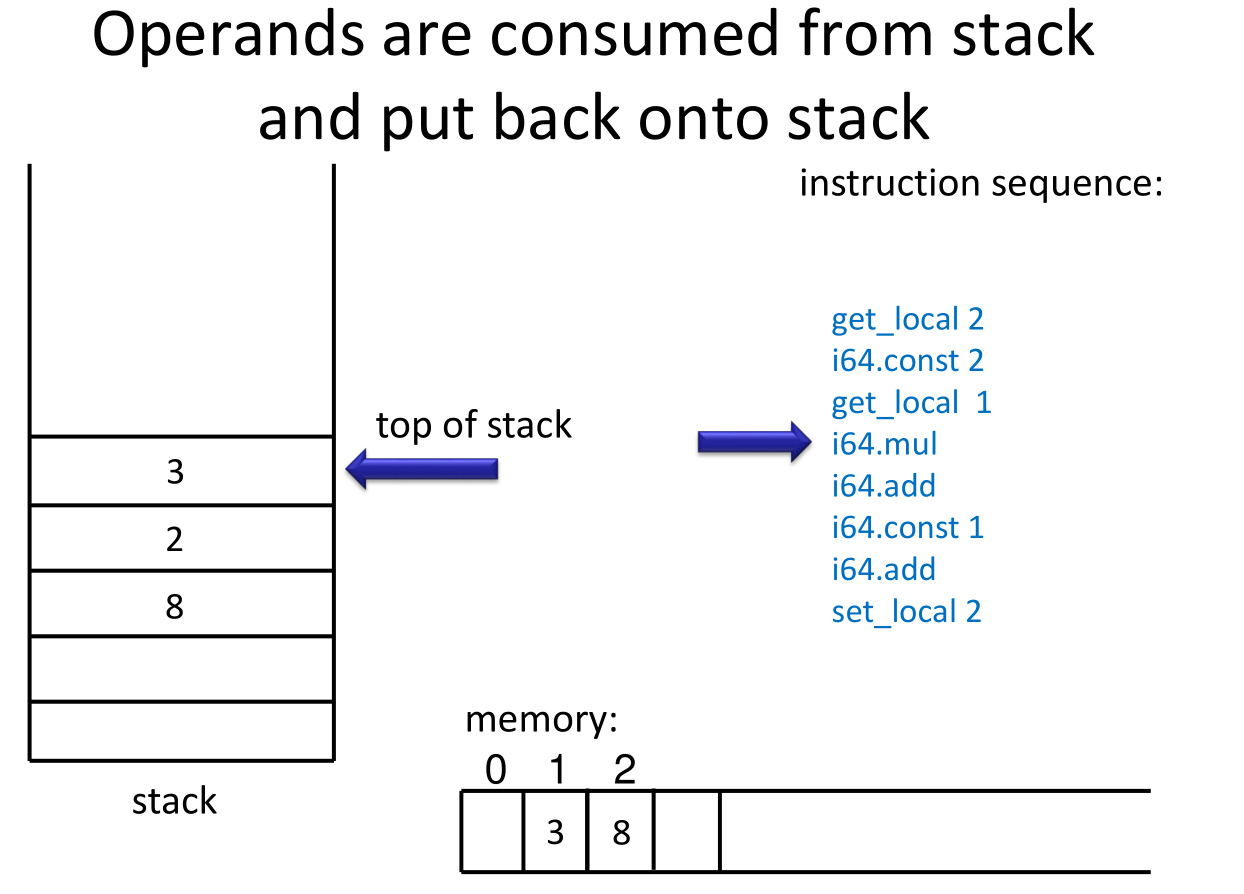
a stack machine simulator could be:
var code : Array[Instruction]
var pc : Int // program counter
var local : Array[Int] // for local variables
var operand : Array[Int] // operand stack
var top : Int
while (true)
step
def step = code(pc) match {
case Iadd() =>
operand(top - 1) = operand(top - 1) + operand(top)
top = top 1 // two consumed, one produced
case Imul() =>
operand(top - 1) = operand(top - 1) * operand(top)
top = top - 1 // two consumed, one produced
case iconst(c) =>
operand(top + 1) = c // put given constant 'c' onto stack
top = top + 1
case Igetlocal(n) =>
operand(top + 1) = local(n) // from memory onto stack
top = top + 1
case Isetlocal(n) =>
local(n) = operand(top) // from stack into memory
top = top 1 // consumed
}
if (notJump(code(n)))
pc = pc + 1 // by default go to next instructions

prefix, postfix, infix notation
let f be a binary operation, e~1~, e~2~ two expressions
- in prefix, f e~1~ e~2~, Polish notation
- in infix, e~1~ f e~2~
- in postfix, e~1~ e~2~ f Reverse Polish notation (RPN)
for nested expressions, like a * b + c, infix needs parentheses, prefix and postfix no bracket
| arg.list | +(x,y) | +(*(x,y),z) | +(x,*(y,z)) | *(x,+(y,z)) |
|---|---|---|---|---|
| prefix | + x y | + * x y z | + x * y z | * x + y z |
| infix | x+y | x*y + z | x + y*z | x*(y+z) |
| postfix | x y + | x y * z + | x y z * + | x y z + ** |
| prefix | + + + x y z u | + x + y + z u |
|---|---|---|
| infix | ((x + y) + z) + u | x + (y + (z + u)) |
| postfix | x y + z + u + | x y z u + + + |
first draw the AST, and then traverse according to the order
below is an example to transform a tree into a prefix, postfix and infix notation:
enum Expr:
case Var(varID: String)
case Plus(lhs: Expr, rhs: Expr)
case Times(lhs: Expr, rhs: Expr)
enum Token:
case ID(str : String)
case Add
case Mul
case O // Opening paren ’(’
case C // Closing paren ’)’
def prefix(e: Expr): List[Token] = e match
case Var(id) => List(ID(id))
case Plus(e1,e2) => List(Add()) ::: prefix(e1) ::: prefix(e2)
case Times(e1,e2) => List(Mul()) ::: prefix(e1) ::: prefix(e2)
def infix(e: Expr): List[Token] = e match // needs to emit parantheses
case Var(id) => List(ID(id))
case Plus(e1,e2) =>
List(O()) ::: infix(e1) ::: List(Add()) ::: infix(e2) :::List(C())
case Times(e1,e2) =>
List(O()) ::: infix(e1) ::: List(Mul()) ::: infix(e2) :::List(C())
def postfix(e: Expr): List[Token] = e match
case Var(id) => List(ID(id))
case Plus(e1,e2) => postfix(e1) ::: postfix(e2) ::: List(Add())
case Times(e1,e2) => postfix(e1) ::: postfix(e2) ::: List(Mul())
Lisp, an example of prefix notation
(defun factorial (n)
(if (<= n 1)
1
(* n (factorial (- n 1)))))
Postscript, an example of post fix language
/inch {72 mul} def
/wedge
{ newpath
0 0 moveto
1 0 translate
15 rotate
0 15 sin translate
0 0 15 sin - 90 90 arc
closepath
} def
gsave
3.75 inch 7.25 inch translate
1 inch 1 inch scale
wedge 0.02 setlinewidth stroke
grestore
gsave
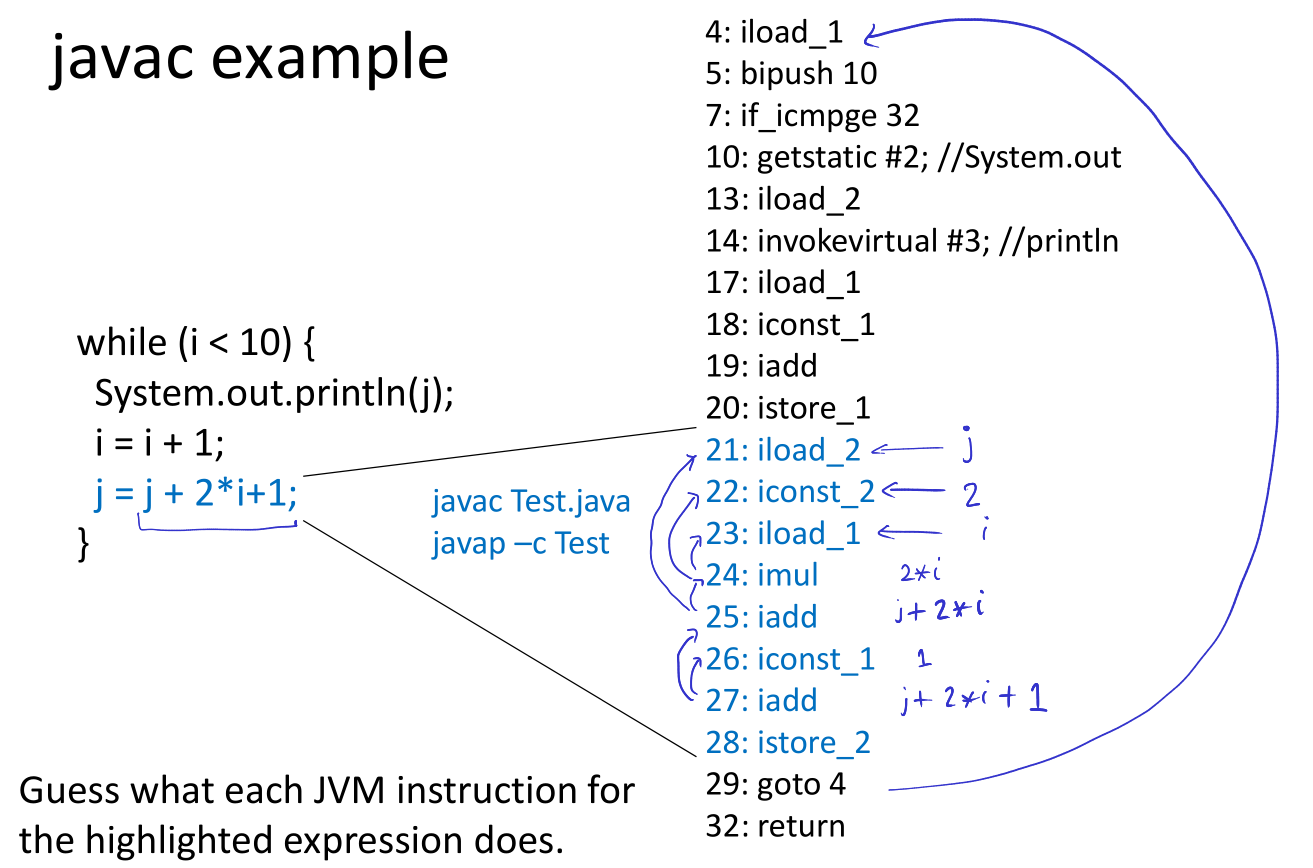
compiling expression
why postfix? can evaluate it using stack
- Evaluating postfix expressions is like running a stack based virtual machine on compiled code
- Compiling expressions for stack machine is like translating expressions into postfix form

to evaluate e1 * e2 interpret as:
- evaluate e1
- evaluate e2
- combines the result using *
def compile(e : Expr) : List[Bytecode] = e match { // ~ postfix printer
case Var(id) => List(Igetlocal(slotFor(id)))
case Plus(e1,e2) => compile(e1) ::: compile(e2) ::: List(Iadd())
case Times(e1,e2) => compile(e1) ::: compile(e2) ::: List(Imul())
}
to include local variables:
- Assigning indices (called slots) to local variables using function slotOf : VarSymbol -> {0,1,2,3,…}
- How to compute the indices?
- assign them in the order in which they appear in the tree
def compile(e : Expr) : List[Bytecode] = e match {
case Var(id) => List(Igetlocal(slotFor(id)))
...
}
def compileStmt(s : Statmt) : List[Bytecode] = s match {
// id=e
case Assign(id,e) => compile(e) ::: List(Iset_local(slotFor(id)))
...
}

compiling control flow:
in Web Assembly, All comparison operators yield 32bit integer results with 1 representing true and 0 representing false.

- block: the beginning of a block construct, a sequence of instructions with a label at the end
- loop: a block with a label at the beginning which may be used to form loops
- br: branch to a given label in an enclosing construct
- br_if: conditionally branch to a given label in an enclosing construct
- return: return zero or more values from this function
- end: an instruction that marks the end of a block, loop, if, or function
block $label1 block $label0
(negated condition code)
br_if $label0 // to else branch
(true case code)
br $label1// done with if
end $label0// else branch
(false case code)
end $label1// end of if
or, in web assembly, it provides a shortcut as:

special tricks for [e1] && [e2]:
| only need to evluate e1 when e1 == False, similarly for [e1] | [e2] when e1 == True |
[if (econd) ethenelse eelse] :=
block nAfter
block nElse
block nThen
branch(econd, nThen, nElse)
end //nThen:
[ethen]
br nAfter
end //nElse:
[eelse]
end //nAfter:
[erest]
branch(!e,nThen,nElse) :=
branch(e,nElse,nThen)
branch(e1 && e2,nThen,nElse) :=
block nLong
branch(e1,nLong,nElse)
end //nLong:
branch(e2,nThen,nElse)
branch(e1 || e2,nThen,nElse) :=
block nLong
branch(e1,nThen,nLong)
end //nLong:
branch(e2,nThen,nElse)
branch(true,nThen,nElse) :=
br nThen
branch(false,nThen,nElse) :=
br nElse
branch(b,nThen,nElse) := (where b is a local var)
get_local #b
br_if nThen
br nElse
we can make a new command as :

then switch statement could write as:
[sswitch] nAfter nBreak :=
block nDefault
block nCasen
...
block nCase1
block nTest
[e_scrutinee] nTest nBreak
end //nTest:
tee_local #s(where s is some fresh local of type i32)
i32.const c1
i32.eq
br_if nCase1
get_local #s
i32.const c2
i32.eq
br_if nCase2
...
br nDefault
end //nCase1:
[e1] nCase2 nAfter
...
end //nCasen:
[en] nDefault nAfter
end //nDefault:
[edefault] nAfter nAfter
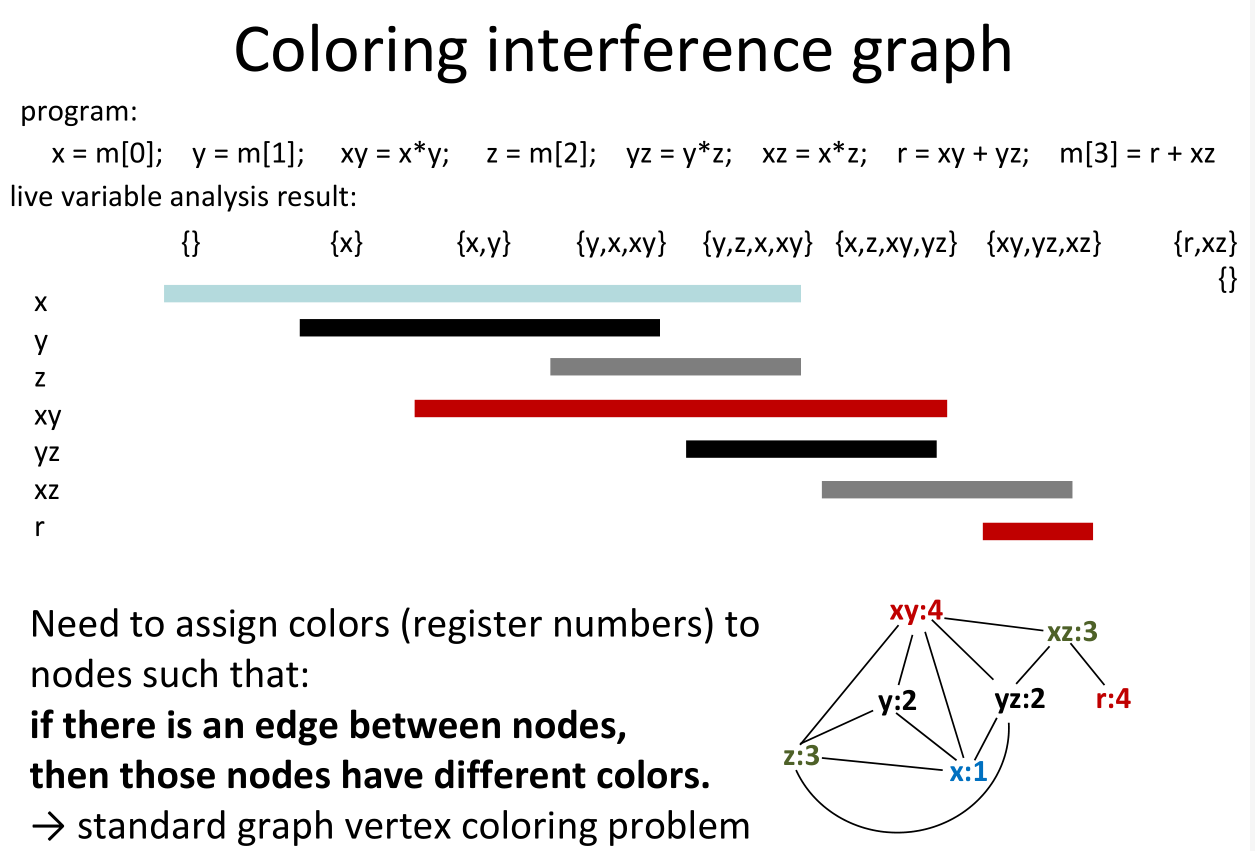
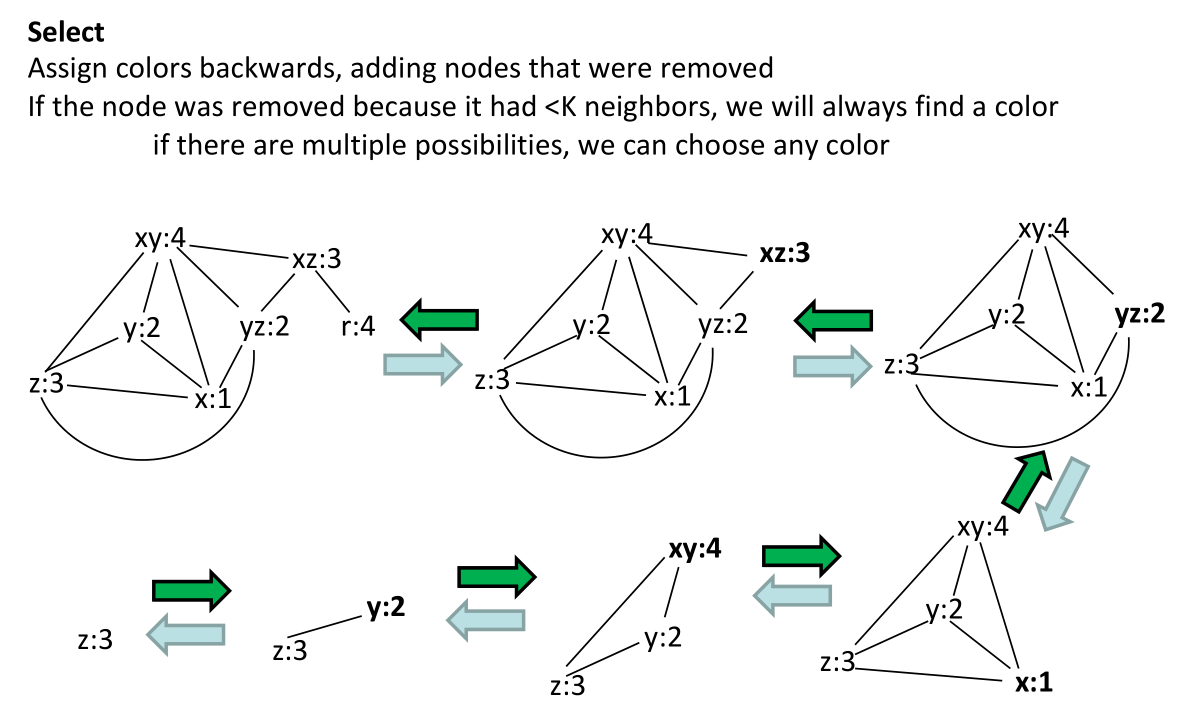
register optimization
Basic Instructions of Register Machines Ri← Mem[Rj] load Mem[Rj] ←Ri store Ri← Rj * Rk compute: for an operation * Efficient register machine code uses as few loads and stores as possible.
wab assembly: imul.32
register machine: R1 ← Mem[SP] SP = SP + 4 R2 ← Mem[SP] R2 ← R1 * R2 Mem[SP] ← R2
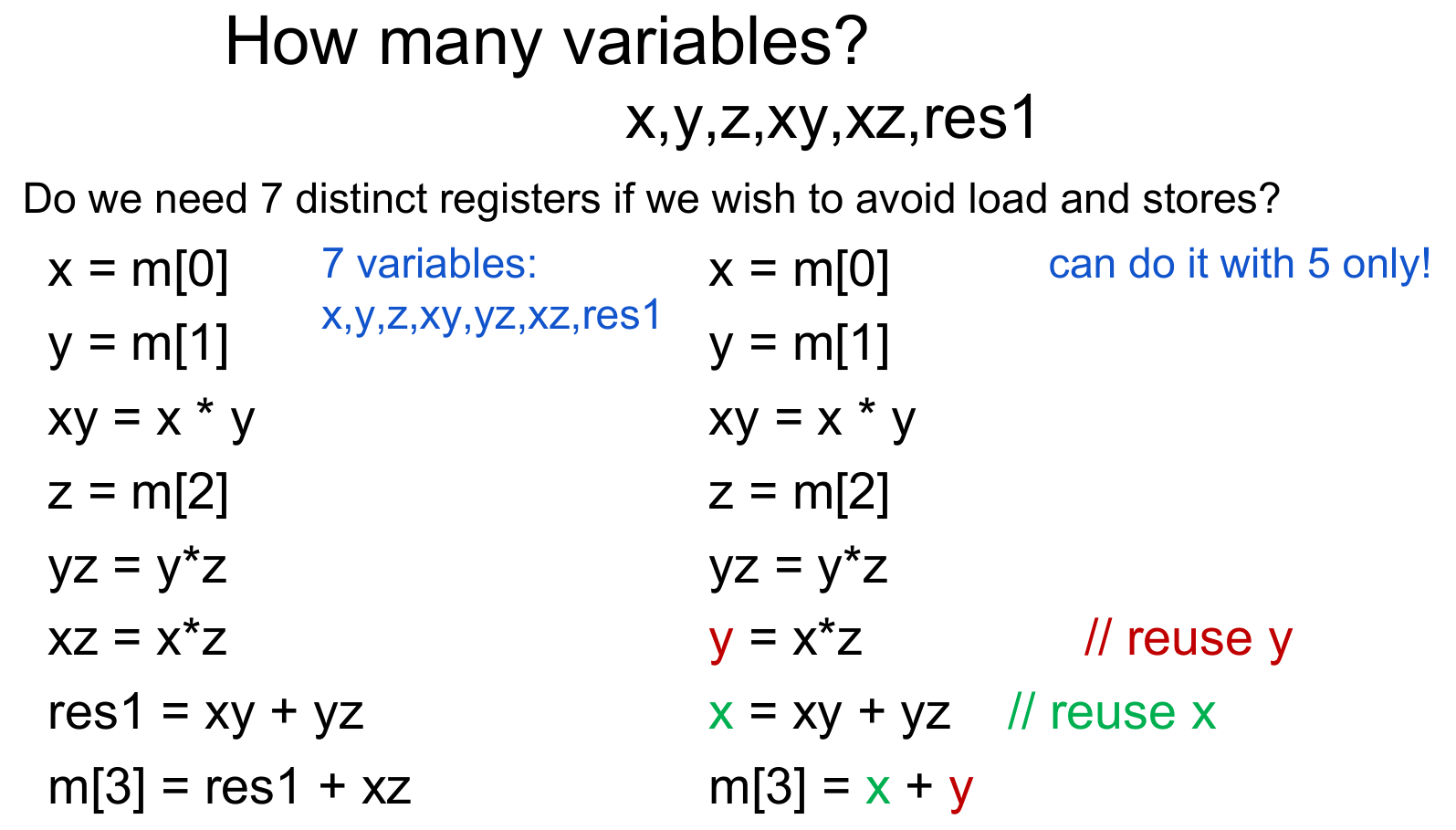

Leave a comment